プラネタリウムアプリの開発で必ず必要になるのが「任意の場所や時刻で、星や惑星がどこに見えているか?」というデータです。あたり前だけど、その計算方法を知らなければ星を正しい位置に描くことができません。
その計算ですが、実はいくつか使える方法あります。これまで私が使ってきたのは、
- 略算式による方法
- ケプラー方程式による方法
- JPL/Caltecの資料による方法
の3つです。それぞれちょこっと紹介しましょう。
略算式による方法
昔に出版された惑星の位置計算本には結構掲載されています。海上保安庁水路部の考案したもので、太陽、月、各惑星の視位置(赤経・赤緯)を一発で計算してくれる便利な計算式です。式は三角関数の羅列(フーリエ級数?)で惑星によってはかなりの項数がありますが、プログラムとして実装しやすい形になっています。
TRIGONOMETRIC SERIES FOR THE COORDINATES OF THE OBJECTS IN THE SOLAR SYSTEM
Yoshio Kubo
海上保安庁 水路研究 No.15 1980
TRIGONOMETRIC SERIES FOR THE COORDINATES OF THE OBJECTS IN THE SOLAR SYSTEM II THE OUTER PLANETS
Toshio Fukushima
海上保安庁 水路研究 No.16 1981
ケプラー方程式による方法
位置計算の基本はこれです。惑星の軌道に関するケプラーの法則から導かれる非線形方程式で、逐次近似によって軌道平面上の位置(動径と角度)を求めることができます。逐次近似はループ処理で書けるので、これもプログラムとして実装しやすいのではないかと思います。これも昔の関連書籍には結構掲載されています。
JPL Caltecの資料による方法
上述のケプラー方程式を使いますが、計算に必要な要素が定数ではなく時間(ユリウス世紀)をパラメータにした変数として与えられます。これによって、過去から未来のかなり広いタイムスパン(紀元前3000年~紀元3000年!)で位置推算ができます。
Keplerian Elements for Approximate Positions of the Major Planets
https://ssd.jpl.nasa.gov/?planet_pos
E.M.Standish
Solar SystemDynamics Group
NASA JPL/Caltech
これまで私は、主に略算式による方法をプログラムライブラリ化して使ってきました。しかし、軌道1周分の位置を求める場合、特に外惑星では何十年、何百年先まで計算することになり、略算式の有効範囲を大きく逸脱するため、計算誤差が大きくなってしまいます。たとえば下の画像を見てください。これは惑星の公転軌道を3次元で描いた例ですが、天王星の軌道が閉じずに(日心黄緯座標のずれが大きくなって)軌道円をうまく描けていないことがわかります。
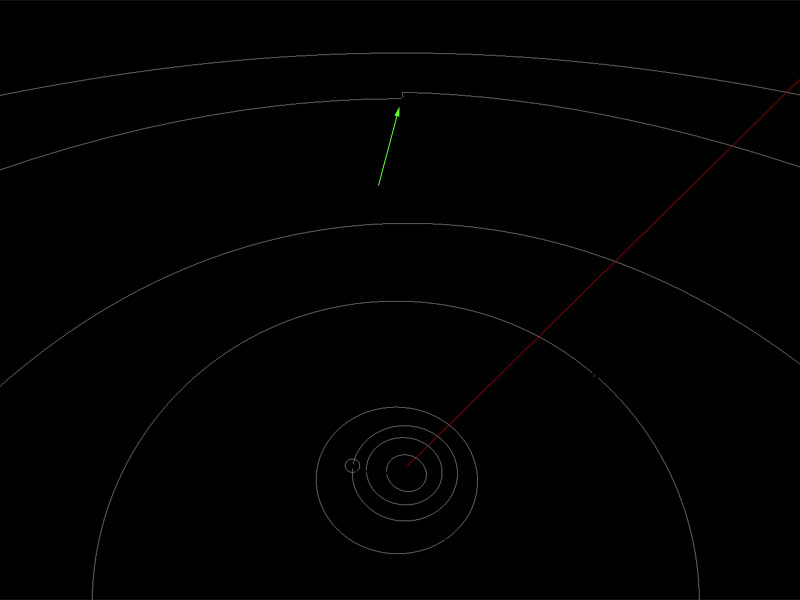
また、冥王星の略算式とJPL/Caltechの計算位置の差異を見ると、大きく両者の計算結果が違うことがわかります。
(現在公開されている資料では、冥王星の計算要素は割愛されています)
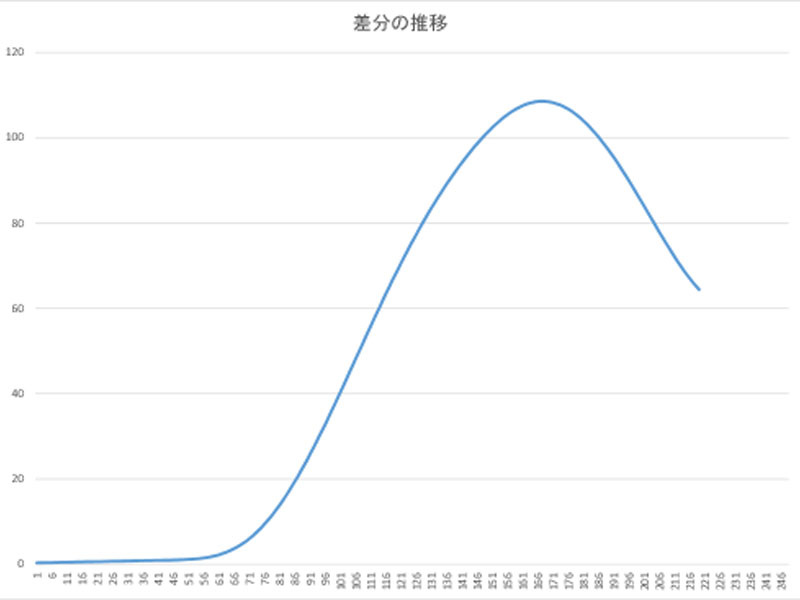
1年毎に位置を計算していくと、60年後を過ぎたあたりから急激に差異が増え、最大で100度以上も計算値が違ってきます。
さらに、略算式では219年くらいで軌道を1周してしまいます。JPL/Caltechでは公転周期の約248年で正しく1周します。
ということで、最近では、長いタイムスパンで位置計算をするときはJPL/Caltechの方法を使うことが多くなりました。
ただ、太陽や月の視位置を直接求められる略算式も便利で捨てがたいです。
(JPL/Caltechの方法では、地球や月の位置は直接計算できず、地球と月の重力中心の位置を求めるようになっています)
そして、いろいろな誤差(惑星光行差、視差、大気差など)を含め、なかなか精度よく求めることができずにけっこう苦労します。フルハイビジョン程度の解像度に描画するならそれほどの精度はいらないのかもしれませんが、やはり精度がよくないと気持ち悪い。メジャーな天文ソフトでは当たり前に解決しているであろう惑星の位置計算ですが、これがイチ素人ではなかなか悩ましい問題なのです。
